дёҖгҖҒе…іиҒ”规еҲҷзҡ„е®ҡд№үе’ҢеұһжҖ§
иҖғеҜҹдёҖдәӣж¶үеҸҠи®ёеӨҡзү©е“Ғзҡ„дәӢеҠЎпјҡдәӢеҠЎ1 дёӯеҮәзҺ°дәҶзү©е“Ғз”ІпјҢдәӢеҠЎ2 дёӯеҮәзҺ°дәҶзү©е“Ғд№ҷпјҢдәӢеҠЎ3 дёӯеҲҷеҗҢж—¶еҮәзҺ°дәҶзү©е“Ғз”Іе’Ңд№ҷгҖӮйӮЈд№ҲпјҢзү©е“Ғз”Іе’Ңд№ҷеңЁдәӢеҠЎдёӯзҡ„еҮәзҺ°зӣёдә’д№Ӣй—ҙжҳҜеҗҰжңү规еҫӢеҸҜеҫӘе‘ўпјҹеңЁж•°жҚ®еә“зҡ„зҹҘиҜҶеҸ‘зҺ°дёӯпјҢе…іиҒ”规еҲҷе°ұжҳҜжҸҸиҝ°иҝҷз§ҚеңЁдёҖдёӘдәӢеҠЎдёӯзү©е“Ғд№Ӣй—ҙеҗҢж—¶еҮәзҺ°зҡ„规еҫӢзҡ„зҹҘиҜҶжЁЎејҸгҖӮжӣҙзЎ®еҲҮзҡ„иҜҙпјҢе…іиҒ”规еҲҷйҖҡиҝҮйҮҸеҢ–зҡ„ж•°еӯ—жҸҸиҝ°зү©е“Ғз”Ізҡ„еҮәзҺ°еҜ№зү©е“Ғд№ҷзҡ„еҮәзҺ°жңүеӨҡеӨ§зҡ„еҪұе“ҚгҖӮ
зҺ°е®һдёӯпјҢиҝҷж ·зҡ„дҫӢеӯҗеҫҲеӨҡгҖӮдҫӢеҰӮи¶…зә§еёӮеңәеҲ©з”ЁеүҚз«Ҝ收ж¬ҫжңә收йӣҶеӯҳеӮЁдәҶеӨ§йҮҸзҡ„е”®иҙ§ж•°жҚ®пјҢиҝҷдәӣж•°жҚ®жҳҜдёҖжқЎжқЎзҡ„иҙӯд№°дәӢеҠЎи®°еҪ•пјҢжҜҸжқЎи®°еҪ•еӯҳеӮЁдәҶдәӢеҠЎеӨ„зҗҶж—¶й—ҙпјҢйЎҫе®ўиҙӯд№°зҡ„зү©е“ҒгҖҒзү©е“Ғзҡ„ж•°йҮҸеҸҠйҮ‘йўқзӯүгҖӮиҝҷдәӣж•°жҚ®дёӯеёёеёёйҡҗеҗ«еҪўејҸеҰӮдёӢзҡ„е…іиҒ”规еҲҷпјҡеңЁиҙӯд№°й“Ғй”Өзҡ„йЎҫе®ўеҪ“дёӯпјҢжңү70 пј…зҡ„дәәеҗҢж—¶иҙӯд№°дәҶй“Ғй’үгҖӮиҝҷдәӣе…іиҒ”规еҲҷеҫҲжңүд»·еҖјпјҢе•Ҷеңәз®ЎзҗҶдәәе‘ҳеҸҜд»Ҙж №жҚ®иҝҷдәӣе…іиҒ”规еҲҷжӣҙеҘҪең°и§„еҲ’е•ҶеңәпјҢеҰӮжҠҠй“Ғй”Өе’Ңй“Ғй’үиҝҷж ·зҡ„е•Ҷе“Ғж‘Ҷж”ҫеңЁдёҖиө·пјҢиғҪеӨҹдҝғиҝӣй”Җе”®гҖӮ
дәҢгҖҒе…іиҒ”规еҲҷзҡ„еә”з”ЁиғҢжҷҜ
иҖҢеңЁе·ҘзЁӢйҖ д»·йўҶеҹҹпјҢж №жҚ®дёҚеҗҢзҡ„жё…еҚ•иҝӣиЎҢз»„д»·пјҢиҖҢз»„д»·зҡ„规еҲҷеҚғеҸҳдёҮеҢ–пјҢеҜ№дәҺдёҖдёӘжңүз»ҸйӘҢзҡ„йў„з®—е‘ҳжқҘиҜҙеҸҜиғҪй©ҫиҪ»е°ұзҶҹпјҢдҪҶжҳҜжҜҸжқЎжё…еҚ•иҝӣиЎҢеӨ„зҗҶд№ҹйңҖиҰҒдёҖе®ҡзҡ„ж—¶й—ҙпјӣиҖҢеҜ№дәҺдёҖеҗҚж–°иҝ‘зҡ„йў„з®—е‘ҳжқҘиҜҙпјҢз»„д»·е°ұдјҡеҸҳеҫ—ејӮеёёзҡ„еӣ°йҡҫгҖӮеӣ жӯӨиҮӘеҠЁпјҲдёҖй”®пјүз»„д»·еҠҹиғҪзҡ„еҠҹиғҪд»·еҖје°ұжӣҙеҠ зҡ„еҮёжҳҫгҖӮ
еңЁе®һзҺ°иҝҷдёӘз®—жі•еүҚжңүеҮ зӮ№еҒҮи®ҫпјҡ
1гҖҒжё…еҚ•гҖҒеӯҗзӣ®ж•°жҚ®е·Із»ҸжӯЈеёёж”¶йӣҶеңЁжҹҗдёҖдёӘDBдёӯпјӣ
2гҖҒе·Із»ҸеҒҡеҘҪеҲқжӯҘеҺ»йҮҚе·ҘдҪңпјӣ
3гҖҒзү№е®ҡйЎ№зӣ®зү№еҫҒпјҢе·ҘдҪңеҶ…е®№з»„еҗҲзҡ„жё…еҚ•е·Із»Ҹжҳ е°„жҲҗе”ҜдёҖдёҖжқЎжё…еҚ•пјҲд»Јз Ғдёӯз®ҖеҚ•зҡ„зҺ°е·Іжё…еҚ•зј–з ҒжқҘиҝӣиЎҢжј”зӨәпјүпјӣ
дёүгҖҒе…іиҒ”规еҲҷзҡ„еә”з”Ёе®һзҺ°
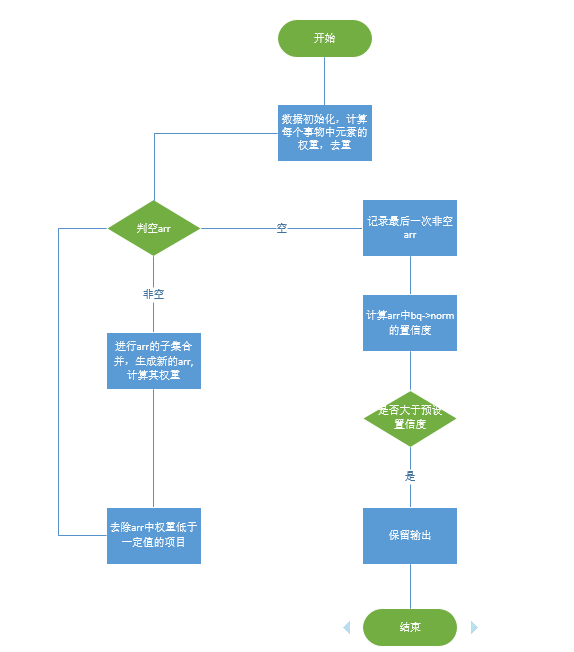
дё»иҰҒеҮҪж•°е®һзҺ°д»Јз Ғпјҡ
// ж•°жҚ®еҲқе§ӢеҢ–пјҢи®Ўз®—жҜҸдёӘе…ғзҙ зҡ„жқғйҮҚпјҢ并еҺ»йҷӨе°ҸдәҺдёҖе®ҡжқғйҮҚзҡ„е…ғзҙ
function InitData(data){
var buffer=[];
var isShow=false;
for (var i = data.length - 1; i >= 0; i--) {
for (var j = data[i].length - 1; j >= 0; j--) {
isShow=false;
for (var k = buffer.length - 1; k >= 0; k--) {
if (buffer[k].name==data[i][j]) {
buffer[k].count++;
isShow=true;
break;
}
}
if (isShow==false) {
buffer.push({
name:data[i][j],
count:1
})
}
}
}
var ret=[];
for (var i = buffer.length - 1; i >= 0; i--) {
if (buffer[i].count>=min_sup) {
ret.push([buffer[i].name]);
}
}
return ret;
}
// и®Ўз®—ж•°з»„дёӯзҡ„еӯҗйӣҶзҡ„жқғйҮҚпјҢиҝӣиЎҢеүӘжһқ
function GenArr(data){
var candi=[];
for(var i=0;i<data.length;i++){
for(var j=i+1;j<data.length;j++){
candi.push(data[i].concat(data[j]).unique());
}
}
candi=unique(candi);
var buffer=[];
for (var i = candi.length - 1; i >= 0; i--) {
buffer.push({arr:candi[i],count:0});
}
//и®Ўз®—жқғйҮҚ
for (var i = buffer.length - 1; i >= 0; i--) {
for (var j = dataArr.length - 1; j >= 0; j--) {
if(isContain(dataArr[j],buffer[i].arr)){
buffer[i].count++;
}
}
}
//еүӘжһқ
var ret=[];
var lock = false;
for (var i = buffer.length - 1; i >= 0; i--) {
if(buffer[i].count>=min_sup){
if (!lock){
result = [];
lock = true;
}
ret.push(buffer[i].arr);
result.push({arr:buffer[i].arr, count:buffer[i].count});
}
}
return ret;
}
еӣӣгҖҒз»“жһңжЈҖи§Ҷпјҡ
Input:
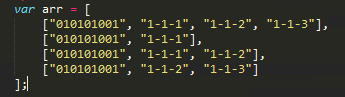
Output:






